Tugas 2. Rangkuman Materi Sistem Bilangan
Tujuan Topik Bahasan
l Mengulas kembali sistem bilangan desimal.
l Menghitung dalam bentuk bilangan biner.
l Memindahkan dari bentuk bilangan desimal ke biner dan dalam biner ke dalam desimal.
l Penggunaan operasi aritmatika pada bilangan biner.
l Menentukan komplemen 1 dan 2 dari sebuah bilangan biner.
l Dan lain – lainnya……..
Sistem Bilangan
Sistem Biner dan Kode – kode digital merupakan dasar untuk komputer dan elektronika digital secara umum. Sistem bilangan biner seperti desimal, hexadesimal dan oktal juga dibahas pada bagian ini. Operasi aritmatika dengan bilangan biner akan dibahas untuk memberikan dasar pengertian bagaimana komputer dan jenis – jenis perangkat digital lain bekerja.
Bilangan Biner
l Sistem Bilangan biner merupakan cara lain untuk melambangkan kuantitas, dimana 1 (HIGH) dan 0 (LOW).
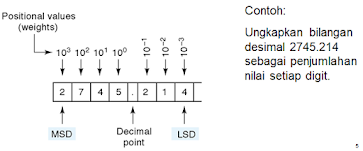
l Sistem bilangan biner mempunyai nilai basis 2 dengan nilai setiap posisi dibagi dengan faktor 2:
Contoh :
Aplikasi Digital
Konversi Desimal ke Biner
l Metode Sum-of-Weight.
l Pengulangan pembagian dengan Metode bilangan 2.
l Konversi fraksi desimal ke biner.
*Metode Sum-of-Weight
Bilangan desimal 9 sebagai The decimal number 9, for example, can be expressed as the sum of binary weight of:
Convert the following decimal numbers to binary:
a) 12 = 1100
b) 25 = 11001
c) 58 = 111010
d) 82 = 1010010
*Repeated Division by 2 Method
*Converting Decimal Fractions to Binary
l Addition, Subtraction, Multiplication, and Division
Binary Addition
Binary Subtraction
Binary Multiplication
The four basic rules for multiplying bits are as follows:
0 X 0 = 0
0 X 1 = 0
1 X 0 = 0
1 X 1 = 1
Binary Division
Division in binary follows the same procedure as division in decimal.
1’s and 2’s Complements of Binary Numbers
l The 1’s and 2’s Complements of Binary Numbers are very important because they permit the representation of negative numbers.
l The method of 2’s compliment arithmetic is commonly used in computers to handle negative numbers
The 1’s complement of a binary number is found by changing all 1s to 0s and all 0s to 1s.
Example:
1 0 1 1 0 0 1 0 (Binary Number)
The 2’s complement of a binary number is found by adding 1 to the LSB of the 1’s complement
2's Complement = (1's Complement) + 1
Example :
Alternative Method to find 2’s Complement
l Start at the right with the LSB and write the bits as they are up and including the first 1
l Take the 1’s complements of the remaining bits
Digital systems, such as the computer, must be able to handle both positive and negative numbers. A signed binary number consists of both sign and magnitude information. The sign indicates whether a number is positive or negative and the magnitude is the value of the number. There three forms in which signed integer (whole) numbers can be represented in binary:
- Sign-Magnitude
- 1’s Complement
- 2’s Complement
Example :
Express the decimal number -39 in sign-magnitude, 1’s complement and 2’s complement,
-39 = 00100111
*Sign-Magnitude:
Decimal Value of positive and negative numbers in the sign-magnitude form are determined by summing the weights in all the magnitude bit positions where there are 1s and ignoring those positions where there are zeros.
*1’s Complement :
Decimal values of negative numbers are determined by assigning a negative value to the weight of the sign bit, summing all the weight where there are 1s and adding 1 to the result
Arithmetic Operations with Signed Number
In this section we will learn how signed numbers are added, subtracted, multiplied and divided. This section will cover only on the 2’s complement arithmetic, because, it widely used in computers and microprocessor-based system .
· *Subtraction
· *Multiplication
· *Division
Hexadecimal Numbers :
l Most digital systems deal with groups of bits in even powers of 2 such as 8, 16, 32, and 64 bits.
l Hexadecimal uses groups of 4 bits.
l Base 16
l 16 possible symbols
l 0-9 and A-F
l Allows for convenient handling of long binary strings.
l Hexadecimal is useful for representing long strings of bits.
l Understanding the conversion process and memorizing the 4 bit patterns for each hexadecimal digit will prove valuable later.
BCD
l Binary Coded Decimal (BCD) is another way to present decimal numbers in binary form.
l BCD is widely used and combines features of both decimal and binary systems.
l Each digit is converted to a binary equivalent.
8 7 4
1000 0111 0100 = 100001110100BCD
l Each decimal digit is represented using 4 bits.
l Each 4-bit group can never be greater than 9.
l Reverse the process to convert BCD to decimal.
l BCD is a decimal number with each digit encoded to its binary equivalent.
l A BCD number is not the same as a straight binary number.
l The primary advantage of BCD is the relative ease of converting to and from decimal.
Alphanumeric Codes
l Represents characters and functions found on a computer keyboard.
l ASCII – American Standard Code for Information Interchange.
l Seven bit code: 27 = 128 possible code groups
l Table 2-4 lists the standard ASCII codes
l Examples of use are: to transfer information between computers, between computers and printers, and for internal storage.
Ditulis : Ananda Bagas Pranata (2F)
Sumber : https://onlinelearning.uhamka.ac.id













Komentar
Posting Komentar